

Now, express the quadratic equation in standard form.Ģx + 1− 2x − 1 = x² − 2 − 2x − 10 = x² − 2x − 3Īpply the quadratic formula in order to identify the roots of the quadratic equation. Substitute the values in the equation 2x + 1 for y in y = x² − 2. The corresponding y-coordinates can be identified with the help of the linear equation.Īnother way of solving the system is to graph the two functions on a similar coordinate plane and then determine the points of intersection.ĭetermine the points of bisection between the line y = 2x + 1 and the parabola y = x² − 2. The solutions to the equation ax² + (b − m)x + (c − d) = 0 will provide us with the x-coordinates of the points of intersection of the graphs of the parabola and the line. Now we have a quadratic equation in 1 variable, the solution of which can be determined with the help of the quadratic formula. Subtract mx+d from both sides of the equation Now, rewrite the new quadratic equation in the standard form. In other words, substitute mx + d for y in y = ax² + bx + c. Substitute the expression for y from the linear equation, into the quadratic equation.

To avoid any sort of confusion with the variables, write the linear equation as y= mx+d where, Note that the standard form of the equation for a parabola with a vertical axis of symmetry is y = ax² + bx + c, a ≠ 0 and the slope- intercept form of the equation for a line is y = mx + b, We can apply a version of the substitution technique in order to solve systems of this type. But what about a system of 2 equations where 1 equation is linear and the remaining is quadratic? You might have solved systems of linear equations.
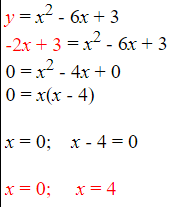
Then, we can also use the x-values and either equation in the system in order to find out the y-values. Hence, we can plug in x + 1 as a substitute for y in the 2 nd equation:įrom here, we are able to solve and simplify the quadratic equation for x, which provides us with the x-values of the solutions to the linear-quadratic system. Simply to say, because the 1 st equation tells us that y is equivalent to x + 1, the y in the 2 nd equation is also equivalent to x + 1. In systems linear quadratic equations, both equations are simultaneously true. In a test, you will be expected to identify the solution(s) to systems either algebraically or graphically.Įxamples of Linear Equation and Quadratic Equationįollowing are the example of Linear and quadratic equations: Since each equation in the system consists of two variables, one way to decrease the number of variables in an equation is by substituting an expression for a variable. The goal of solving systems linear quadratic equations is to significantly reduce two equations having two variables down to a single equation with only one variable. Linear and quadratic equations are the algebraic systems of equations consisting of one linear equation and one quadratic equation.


 0 kommentar(er)
0 kommentar(er)
